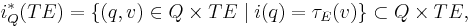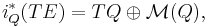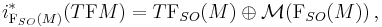Kosmann lift
In differential geometry, the Kosmann lift,[1][2] named after Yvette Kosmann-Schwarzbach, of a vector field 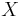 on a Riemannian manifold
on a Riemannian manifold 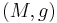 is the canonical projection
is the canonical projection 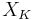 on the orthonormal frame bundle of its natural lift
on the orthonormal frame bundle of its natural lift 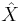 defined on the bundle of linear frames.[3]
defined on the bundle of linear frames.[3]
Generalisations exist for any given reductive G-structure.
Contents |
Introduction
In general, given a subbundle 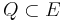 of a fiber bundle
of a fiber bundle 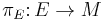 over
over  and a vector field
and a vector field 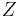 on
on  , its restriction
, its restriction 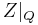 to
to  is a vector field "along"
is a vector field "along"  not on (i.e., tangent to)
not on (i.e., tangent to)  . If one denotes by
. If one denotes by 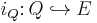 the canonical embedding, then
the canonical embedding, then 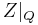 is a section of the pullback bundle
is a section of the pullback bundle 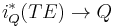 , where
, where
and 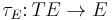 is the tangent bundle of the fiber bundle
is the tangent bundle of the fiber bundle  . Let us assume that we are given a Kosmann decomposition of the pullback bundle
. Let us assume that we are given a Kosmann decomposition of the pullback bundle 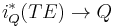 , such that
, such that
i.e., at each 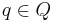 one has
one has 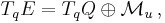 where
where 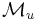 is a vector subspace of
is a vector subspace of 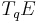 and we assume
and we assume 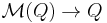 to be a vector bundle over
to be a vector bundle over  , called the transversal bundle of the Kosmann decomposition. It follows that the restriction
, called the transversal bundle of the Kosmann decomposition. It follows that the restriction 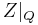 to
to  splits into a tangent vector field
splits into a tangent vector field 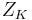 on
on  and a transverse vector field
and a transverse vector field 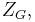 being a section of the vector bundle
being a section of the vector bundle 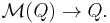
Definition
Let 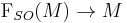 be the oriented orthonormal frame bundle of an oriented
be the oriented orthonormal frame bundle of an oriented  -dimensional Riemannian manifold
-dimensional Riemannian manifold  with given metric
with given metric 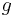 . This is a principal
. This is a principal 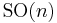 -subbundle of
-subbundle of 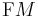 , the tangent frame bundle of linear frames over
, the tangent frame bundle of linear frames over  with structure group
with structure group 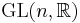 . By definition, one may say that we are given with a classical reductive
. By definition, one may say that we are given with a classical reductive 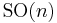 -structure. The special orthogonal group
-structure. The special orthogonal group 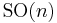 is a reductive Lie subgroup of
is a reductive Lie subgroup of 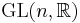 . In fact, there exists a direct sum decomposition
. In fact, there exists a direct sum decomposition 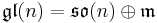 , where
, where 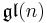 is the Lie algebra of
is the Lie algebra of 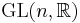 ,
, 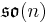 is the Lie algebra of
is the Lie algebra of 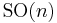 , and
, and 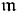 is the
is the 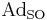 -invariant vector subspace of symmetric matrices, i.e.
-invariant vector subspace of symmetric matrices, i.e. 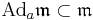 for all
for all 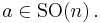
Let 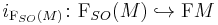 be the canonical embedding.
be the canonical embedding.
One then can prove that there exists a canonical Kosmann decomposition of the pullback bundle 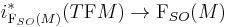 such that
such that
i.e., at each 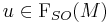 one has
one has 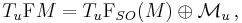
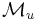 being the fiber over
being the fiber over  of the subbundle
of the subbundle 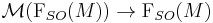 of
of 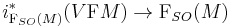 . Here,
. Here, 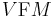 is the vertical subbundle of
is the vertical subbundle of 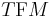 and at each
and at each 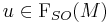 the fiber
the fiber 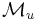 is isomorphic to the vector space of symmetric matrices
is isomorphic to the vector space of symmetric matrices 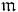 .
.
From the above canonical and equivariant decomposition, it follows that the restriction 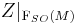 of an
of an 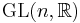 -invariant vector field
-invariant vector field 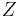 on
on 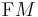 to
to 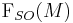 splits into a
splits into a 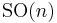 -invariant vector field
-invariant vector field 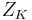 on
on 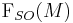 , called the Kosmann vector field associated with
, called the Kosmann vector field associated with 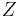 , and a transverse vector field
, and a transverse vector field 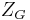 .
.
In particular, for a generic vector field 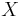 on the base manifold
on the base manifold 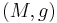 , it follows that the restriction
, it follows that the restriction 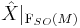 to
to 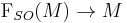 of its natural lift
of its natural lift 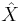 onto
onto  splits into a
splits into a 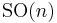 -invariant vector field
-invariant vector field 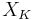 on
on 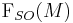 , called the Kosmann lift of
, called the Kosmann lift of 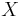 , and a transverse vector field
, and a transverse vector field 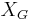 called the von Göden lift of
called the von Göden lift of 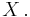
See also
- Frame bundle
- Orthonormal frame bundle
- Principal bundle
- Spin bundle
- Connection (mathematics)
- G-structure
- Spin manifold
- Spin structure
Notes
- ^ Fatibene L., Ferraris M., Francaviglia M. and Godina M. (1996), A geometric definition of Lie derivative for Spinor Fields, in: Proceedings of the 6th International Conference on Differential Geometry and Applications, August 28th– September 1st 1995 (Brno, Czech Republic), Janyska J., Kolář I. & J. Slovák J. (Eds.), Masaryk University, Brno, pp. 549–558
- ^ Godina M. and Matteucci P. (2003), Reductive G-structures and Lie derivatives, Journal of Geometry and Physics 47, 66–86
- ^ Kobayashi, Shoshichi; Nomizu, Katsumi (1996), Foundations of Differential Geometry, Vol. 1, Wiley-Interscience, ISBN 0470496479 (Example 5.2) pp. 55-56
References
- Kobayashi, Shoshichi; Nomizu, Katsumi (1996), Foundations of Differential Geometry, Vol. 1 (New ed.), Wiley-Interscience, ISBN 0471157333
- Kolář, Ivan; Michor, Peter; Slovák, Jan (1993) (PDF), Natural operators in differential geometry, Springer-Verlag, http://www.emis.de/monographs/KSM/kmsbookh.pdf
- Sternberg, S. (1983), Lectures on Differential Geometry (2nd ed.), New York: Chelsea Publishing Co., ISBN 0-8218-1385-4
- Fatibene, Lorenzo; Francaviglia, Mauro (2003), Natural and Gauge Natural Formalism for Classical Field Theories, Kluwer Academic Publishers, ISBN 978-1402017032